Коэффициент корреляции в Excel (и корреляционная матрица)
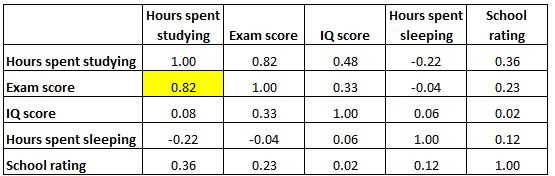
Существует множество методов, позволяющих измерить степень взаимосвязи переменных. Один из самых распространенных инструментов для этого — коэффициент корреляции. Он позволяет определить, насколько тесно связаны между собой две переменные и выявить, существует ли между ними линейная зависимость. Коэффициент корреляции может принимать значения от -1 до 1, где -1 указывает на полностью обратную зависимость, 0 — на отсутствие связи, а 1 — на полностью прямую связь.
Использование специальных инструментов для анализа данных, таких как Microsoft Excel, облегчает вычисление коэффициента корреляции и дает возможность визуализации полученных результатов. Анализ корреляций может быть основой для принятия важных решений во многих областях, от науки и исследований до бизнеса и финансов. Давайте ближе познакомимся с этим мощным инструментом и его возможностями в контексте Microsoft Excel.
Как использовать и интерпретировать результаты анализа взаимосвязи данных на примере Excel
Анализ взаимосвязи данных может быть важным инструментом для исследования зависимостей и понимания влияния одной переменной на другую в наборе данных. В Excel существует возможность провести такой анализ с помощью коэффициента корреляции, который позволяет измерить степень связи между двумя переменными.
Перед использованием коэффициента корреляции в Excel необходимо подготовить данные, выбрав соответствующие переменные для анализа. После этого можно приступить к расчету коэффициента, который позволяет определить силу и направление связи между переменными. Важно помнить, что коэффициент корреляции не указывает на причинно-следственную связь между переменными, а лишь показывает, насколько они связаны друг с другом.
Интерпретация коэффициента корреляции может быть ключевым шагом в анализе данных. Положительное значение коэффициента указывает на прямую зависимость между переменными, то есть, при увеличении значения одной переменной, увеличивается и значение другой переменной. Отрицательное значение коэффициента, наоборот, указывает на обратную зависимость, то есть, при увеличении значения одной переменной, значение другой переменной уменьшается.
Коэффициент корреляции также может принимать значение от -1 до 1, где ближе значение к -1 или 1, тем сильнее связь между переменными. Значение ближе к 0 указывает на отсутствие или очень слабую связь.
Важно отметить, что интерпретация коэффициента корреляции должна основываться на полученных данных. Значительные отклонения от ожидаемых результатов могут указывать на наличие других факторов, влияющих на взаимосвязь переменных, которые не были учтены в анализе.
Таким образом, использование и интерпретация коэффициента корреляции в Excel позволяет исследовать связь между переменными и получить представление о степени их взаимосвязи. Однако, важно помнить, что коэффициент корреляции не может быть использован как основа для создания причинно-следственных связей между переменными.
Корреляционная матрица в Excel: инструмент анализа и визуализации данных
В данном разделе рассматривается функционал корреляционной матрицы в программе Excel, который представляет собой мощный инструмент для анализа и визуализации данных. Он позволяет изучить связи между различными показателями, выявить тенденции и зависимости, а также прогнозировать будущие тренды.
- Преимущества использования корреляционной матрицы
- Алгоритм создания корреляционной матрицы в Excel
- Визуализация корреляционной матрицы с помощью диаграмм и графиков
- Интерпретация результатов и примеры практического применения
- Рекомендации по использованию корреляционной матрицы для принятия решений
Одной из главных преимуществ корреляционной матрицы является возможность выявить связи и зависимости между переменными без предварительного знания о них. Корреляционная матрица позволяет оценить степень связи между различными параметрами и определить их влияние на исследуемый процесс или явление. С помощью этого инструмента можно выявить наличие положительной, отрицательной или нулевой корреляции, что позволяет прогнозировать возможные изменения и принимать обоснованные решения.
Для создания корреляционной матрицы в Excel следует выполнить несколько шагов, включающих выделение используемых параметров и ввод формулы для расчета корреляции. После получения результатов можно перейти к их визуализации с помощью диаграмм и графиков, что позволит более наглядно представить данные и обнаружить возможные закономерности.
Интерпретация результатов корреляционной матрицы требует глубокого понимания показателей и их взаимосвязей. Рассмотрение примеров практического использования корреляционной матрицы поможет разобраться в методологии анализа данных и применить ее для конкретных задач.
Важно учитывать, что корреляционная матрица не дает причинно-следственных связей между переменными, но позволяет выявить взаимосвязь. Правильное использование данного инструмента способствует принятию обоснованных решений и оптимизации процессов на основе анализа данных.
Как создать и интерпретировать таблицу взаимосвязи факторов в Excel
Для создания таблицы взаимосвязи факторов в Excel, необходимо использовать функцию корреляции. Функция корреляции позволяет определить степень линейной связи между двумя переменными и вычислить коэффициент корреляции. Полученные значения коэффициента корреляции помещаются в ячейки таблицы, которая представляет собой матрицу взаимосвязи факторов.
| Фактор 1 | Фактор 2 | Фактор 3 | |
|---|---|---|---|
| Фактор 1 | 1.00 | 0.75 | 0.40 |
| Фактор 2 | 0.75 | 1.00 | 0.60 |
| Фактор 3 | 0.40 | 0.60 | 1.00 |
Интерпретация полученных значений таблицы взаимосвязи факторов позволяет определить степень связи между каждым из факторов. Значения коэффициента корреляции могут варьироваться от -1 до 1. Значение близкое к 1 указывает на положительную линейную связь между факторами, в то время как значение близкое к -1 указывает на отрицательную линейную связь. Значение близкое к 0 указывает на отсутствие линейной связи.

Похожие записи: